
This post was originally written as a speech given in Chinese at the Papers We Love meetup in Taipei. The Chinese version can be found here and the recording here.
Introduction
Today I'll talk to you about cooperation. What is it? Why do people decide to cooperate with each other, even when it is in their interest not to? How can we analyze the conditions under which it arises?
This talk is based on the classic book, Evolution of Cooperation by Axelrod (1984). We'll start by looking at some examples, how we can use game theory and "Prisoner's dilemma" to think about them. Then we'll look at under what conditions cooperation can arise, and what makes tit for tat such an effective strategy.
Next post we'll look at how these lessons are applied in a modern system in the form of Bittorrent, a p2p file sharing protocol, to encourage people to share with each other.
After this, you should have a better understanding of how cooperation can arise, what conditions are useful for it, and how to think about it in game theoretical terms.
Trench warfare
During World War 1, countries in Europe on the western front engaged in trench warfare. One curious dynamic that emerges is that the soldiers often didn't shoot to kill each other. How come this "Live and let live" dynamic emerged in the most violent setting imaginable, in the middle of a world war where it was either you or your enemy who survived?
One thing that is very different with trench warfare from previous forms of warfare is that the same small group of soldiers are usually stuck in the same place for months. This means they'll have many opportunities to engage with the enemy. As it turns out, repeated exposure is key for cooperative behavior to emerge. It turns a prisoner's dilemma into an iterated prisoner's dilemma. We'll have a closer look at this later.

What ended up happening is that neither side wanted to attack, because they knew there would be retaliation and they'd both be better of if things stayed peaceful. Note that this only applied on a small scale with small groups where the "enemy" was someone they interacted with daily over the course of a long period of time. It didn't apply to the larger battle field, nor did it apply to the higher ranking officers who made plans to attack.
There are some amusing anecdotes from various war journals at the time. Here are a few:
- During Christmas in 1914 English and German soldiers entered no man's land to play football with each other. (the movie Joyeux Noel)
- British hear gunshots, starts yelling at the Germans and German soldiers apologize and hope no one was hurt, blaming "the damned Prussian artillery"
- The British had an "evening gun" that was fired at the exact same spot exactly at 7pm, as a predictable form of "aggression".

Basically, anything except trying to destroy the enemy. Of course, sometimes the higher up officers forced invasion, accidents happened, a new group arrived, or some people felt particularly blood thirsty. In those cases, retaliation was swift and brutal. Often the retaliation, the counter attack, was worse than the initial attack. This worked as a form of deterrence. In practice what was taking place was the organic development of a tit-for-tat strategy across many places in the western front.
Let's look at the underlying dynamics of this, in order to understand it better.
Prisoner's dilemma
How does a tit-for-tat strategy, like the one we saw above, emerge when we model the situation as a game?
In the field of game theory there's a famous example called Prisoner's dilemma. The setup is as follows. You have two prisoner's who both risk going to jail. They can choose to stay silent (cooperate) or betray (defect) their partner. If they both cooperate, they both get 1 year jail time. If one stays silent and the other betrays, the person staying silent gets 3 year jail time and the other one goes free. If they both betray each other they each get two years in jail.
The dilemma is as follows: the best collective outcome for them both is to cooperate, in which case they get 1 year jail time each. However, acting in self-interest and to avoid jail time, the dominant strategy, a strategy that is better regardless of what another player choose, is that they both betray each other. This means they both get 2 years jail time, which is obviously worse. Hence the dilemma.
We can capture this in a payoff matrix, with each player's options and consequences in a table.
| Alice/Bob | Cooperate | Defect |
|---|---|---|
| Cooperate | -1 /-1 | -3 / 0 |
| Defect | 0 / -3 | -2 / -2 |
Formally, a game is called a prisoner's dilemma if the following holds:
| Alice/Bob | Cooperate | Defect |
|---|---|---|
| Cooperate | R | S |
| Defect | T | P |
where R=reward, T=temptation, S=sucker, P=punishment and you have T>R>P>S. You also need 2R>T+S, to ensure mutual cooperation is preferable over taking turns cooperating and defecting. This means it is worth defecting if the other person is cooperating, and it is worth defecting if the other person is defecting as well.
Is there any way out of this dilemma? It turns out there is if you play the game many times. Before we look at this, let me show you two more examples of prisoner's dilemma.
The first is peace war game, which is the same expect you decide whether to have peace of war. Notice how this is similar to what we saw in the beginning with trench warfare, where collectively they found a way to keep peace, for the most part anyway.
| Alice/Bob | Peace | War |
|---|---|---|
| Peace | 2 / 2 | 0 / 3 |
| War | 3 / 0 | 1 / 1 |
The other is a subset of Prisoner's dilemma called a "donation game". In it you can give something at cost c and that gives benefit b to the other person, with b>c. This is often used to model markets where you have some form of trade.
| Alice/Bob | Cooperate | Defect |
|---|---|---|
| Cooperate | b-c / b-c | -c / b |
| Defect | b / -c | 0 / 0 |
Notice that b>(b-c)>0>-c and 2(b-c)>b-c, hence it is a form of prisoner's dilemma.
4) Axelrod's tournament
How can we encourage cooperation and where does tit-for-tat emerge? One way is to play a game many times. Why does this help?
If you play many games in a row with the same player, you can choose how you act each round based on what the other player did. You can have conditional strategies. Which strategy is the best? There is no single best strategy, as it depends on the environment and what strategies other players choose. But one strategy that work very well in most circumstances of repeated games is tit for tat. This is captured in many sayings around mutual reciprocation, such as "a tooth for a tooth", "live and let live". It basically says: start by cooperating, then follow the other player's move. If the other player cooperates, you cooperate. If they defect, you defect. And so on.
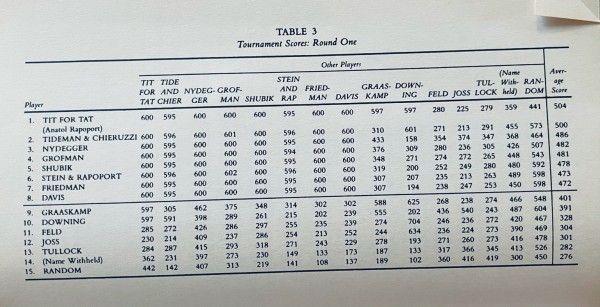
Axelrod arranged a famous computer tournament in 1980 with many programs competing against each other playing several rounds. These were submitted by people from all over the world. Tit for tat performed the best.
Why is this? To get an intuition, consider a situation in which three types of players exists, one with TIT FOR TAT strategy, one with always defecting strategy, ALL D, and another one who is always cooperating, ALL C.
The first player would initially get some benefit, but would quickly get punished by other players, such as TIT FOR TAT, meaning its overall score would be lower. Similarly, ALL C would be taken advantage over, and run over again and again. Meanwhile, TIT FOR TAT playing against someone with a similar strategy would cooperate most of the time and get a high score.
5) More on Tit for tat
We discover that certain attributes are more useful than others for survival. For example, being "nice", as in never defecting first. All of the top 8 strategies in the tournament were nice.
Two other attributes are worth mentioning. One is "retaliation", as in punishing someone who is defecting. The other is "forgiveness", where you "let bygones by bygones", which means cooperation can arise again if a party chooses to resume cooperation. The concept of forgiveness also becomes especially interesting in an environment where there is a noisy channel, and we can't always interpret clearly if an action is a form of defection or not, which leads to alternative strategies such as "tit for two tats".
Another thing worth noting is how short the tit for tat strategy is. If we describe it as a computer program, it is very easy to understand. This also make it transparent and clear, i.e. an opponent can easily infer what strategy is being used after playing for a bit, which in turn makes cooperation more likely to develop. We call this property "clarity".
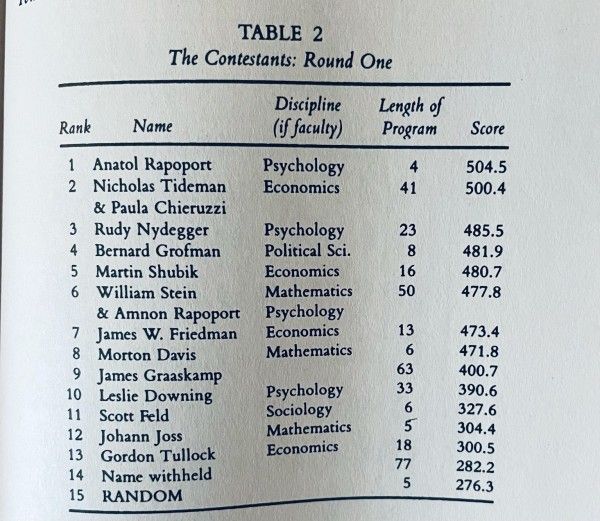
In summary, tit for tat is nice, forgiving, retaliatory and clear, and this makes it robust and able to thrive in many environments.
After the tournament, there was a second tournament where people could learn from the mistakes done in the first tournament to come up with better strategies. An interesting piece of information is that even when there was a second tournament, and people knew tit-for-tat would compete, no other strategy managed to perform better than it!
If you are interested in developing intuition for this, and play around with it more, there's a great game that you can play that is also based on this book. You can find it here: https://ncase.me/trust/
In the next post, we'll look at these insights can be used in designing computer systems, specifically how it is used in Bittorrent.
Acknowledgements
Thanks to Sanaz for comments on this post, and my Chinese teacher Jenny for comments and much help with the Chinese version.
Subscribe to Gaptry
Subscribe to the newsletter and unlock access to member-only content.